Meta-learning in finance: boosting models calibration with deep learning

Hi everyone! Recently I completed MSc in mathematics at the University of Verona, where I started to work on the intersection of financial engineering and machine learning with the help of my supervisor Luca Di Persio. You can find some of the works related to financial time series forecasting in my blog, but this article will be related to a somewhat different issue. In my masters' thesis, I researched the idea of boosting financial models calibration using deep neural networks as approximators of other optimization algorithms. I could show for several basic models, like Black-Scholes and Merton jump models, that we can speed up the calibration process in thousands of times while having very negligible loss of accuracy. In this article, I’ll present the idea behind this work, connections to meta-learning and perspectives of this approach. You can find the .pdf manuscript of the thesis itself here.
Why meta-learning?
In terms of modern AI, “learning” usually means optimizing some cost function, that validates the performance of a machine learning model. We maximize likelihood in Bayesian models, minimize mean squared error with gradient descent in neural networks, or maximize expected rewards in the reinforcement learning framework. For every new problem, we repeatedly re-run this optimization routine, which often takes a lot of computational time. What if we could “learn” the “learning process” at least for similar problems to avoid re-running optimization from scratch?

This is a very active area of research, driven by big industrial labs like DeepMind, Berkley, OpenAI, and others. I decided to try this idea on my own, while the learning process of my interest became financial model calibration routine, that is a crucial task, that, from my point of view, definitely requires improvements.
Financial model calibration
Mathematical model supposed to describe or explain some real-world object or process based on the input parameters and their connections, defined by human experts. For example, we can describe the motion of physical objects knowing their mass, position and movement speed, and mathematicians combined these variables into differential equations within Newtonian / Lagrangian / Hamiltonian mechanics. But since we’re interested to understand real-world motion, we need to find such parameters of speed, mass etc that correspond to the empirical observations. The process of minimizing the error between these observations and outputs of the mathematical model with respect to its parameters is called model calibration.
Financial models are working in the same way. In my research, I worked with mathematical models for option pricing, where I had to fit empirical option prices from the market to the valuations of the Black-Scholes or Merton jump model with respect to their parameters, like volatility, jump intensity etc.

Usually, this problem is solved with gradient-based approaches, if closed-form solution is available (like the case of Black-Scholes model), but in case of sophisticated models that don’t allow closed-form solution and are used alongside with Monte-Carlo simulations, heuristical algorithms, like evolutionary algorithms are being applied. Hence, within the meta-learning framework, I am interested in the replication of these “heavy” optimization algorithms, that optimize for minutes, or, probably, hours, with a simple neural network that does inference in less than one second.
Machine learning for model calibration
My neural network supposed to “copy” optimization process of finding optimal parameters of a mathematical model. Hence, the outputs are clear, but what are the inputs then? In our case, we will predict these parameters based on 1) market prices of the options themselves, 2) properties of these options (like strike price or time-to-maturity), and 3) exogenous variables, that can be market sentiment or open interest.
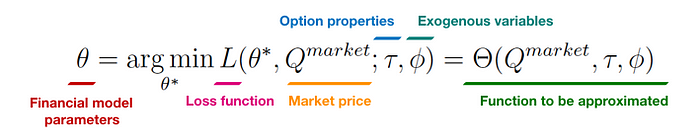
An unobvious problem that occurs here related to the data. We can calibrate our model with a “slow” algorithm (I used differential evolution with is implemented in SciPy) for a couple of years of options trades, which still will be not enough since we need tens of thousands example to fit an ML model. The interesting trick to solve it was offered in this paper, namely, we can sample parameters randomly, pass them into a mathematical model and obtain option prices that “could have been true” if input parameters were correct with respect to this market. This way we can create as many as we want artificial examples of priced options, and for the exogenous variables, we can fit a regression model to recover them from prices as well.
Unfortunately, I am not able to share the data I used for the research and the code without the corresponding data will not be particularly useful. I can show you the neural network architecture, but there is nothing you already don’t know:
def dense_bn_block(inn, size):
x = Dense(size, activation='linear')(inn)
x = BatchNormalization()(x)
x = Activation('relu')(x)
return xdef residual_block(inn, size):
x = dense_bn_block(inn, size)
x = add([inn, x])
return xinputs = Input(shape=(295, ))
x = GaussianNoise(0.05)(inputs)
x = BatchNormalization()(x)
for i in range(1, 5):
x = residual_block(x, 64)
x = Dropout(0.25)(x)
predictions = Dense(1, activation='linear')(x)
model = Model(inputs=inputs, outputs=predictions)
I also have used the codes for stochastic processes and market structure from this amazing book.
Understanding results
Now, the most interesting part. Did it really work? On the table below, there are MAEs and times for differential evolution (DE) optimization and neural network based (NN) optimization for two models of interest.

We can see, that computational speedup is indeed very significant, but let’s check MAEs visually too. On the picture below black like represents errors for the DE algorithm, blue line — NN errors in train set and orange one — in the test set. It looks rather adequate for the Black-Scholes model, where a single parameter, volatility, had to be found.

Situation changes with Merton jump model. We can see, that DE performed much worse than in the case of the Black-Scholes model because optimizing for 4 parameters is a much more difficult problem. But thanks to the artificially generated examples in the training dataset, the neural network could learn correct patterns, hence, performing even better than the reference optimization algorithm it aimed to approximate!

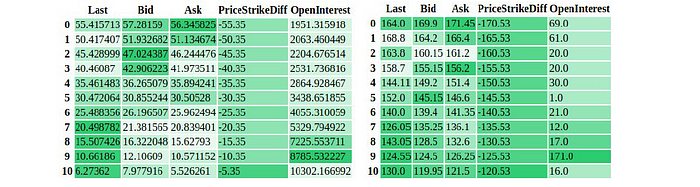
I also have played with visual sensitivity analysis of the models, being inspired by interpretation algorithms used in computer vision, that are implemented in this Python library. On the image below you can see samples from the two option chains, where on the left one just a couple of important options are highlighted, while on the right one almost every variable is important, i.e., in this case, the neural network is too sensitive to the perturbations of the input, and, hence, needs to be retrained. Check more details in the thesis manuscript.
Conclusion
As for me, this research opens numerous practical applications for neural networks in a very different way. Instead of learning them to classify/do the regression as we used to, we can approximate functions, or, even better, approximate the final results of complex stochastic processes as iterative optimization. I am planning to extend the obtained results to different mathematical models and different datasets, expecting the same good results. It’s also very interesting to apply reinforcement learning to model optimization process. Last but not least, I would like to try this approach in other industries, where decisions are driven by mathematical models that need to be calibrated.
P.S.
Follow me also on Facebook for AI articles that are too short for Medium, Instagram for personal stuff and Linkedin! Contact me if you want to collaborate on the intersection of finance and machine learning or other ML projects.
